최단경로 알고리즘
그래프 상에서 가장 짧은 경로를 찾는 알고리즘
최단경로를 찾는 알고리즘으로는 다익스트라 알고리즘과 플로이드 워셜 알고리즘, 벨만포드 알고리즘이 있다
종류
- 한 지점에서 다른 특정 지점까지의 최단 경로
- 모든 지점에서 다른 모든 지점까지의 최단 경로 모두 구하기 등이있음
표현 방법
- 그래프로 표현하며 각 지점은 그래프에서 노드로 표현되고, 지점간 연결된 도로는 그래프에서 간선으로 표현됨

다익스트라 알고리즘
'단계마다 방문하지 않은 노드 중에서 가장 최단 거리가 짧은 노드'를 선택한 뒤에 그 노드를 거쳐가는 경우를 확인해 최단 거리를 갱신하는 방법
우선순위 큐를 이용해 소스코드를 작성해야 효율적이다
- 역할 : 한 지점에서 다른 모든 지점까지의 최단 경로를 계산합니다
- 음의간선(0보다 작은 값을 가지는 간선)이 없을 경우에만 정상적으로 작동
- 보통 GPS 소프트웨어의 기본 알고리즘으로 채택됨
- 다익스트라는 그리디 알고리즘으로 분류된다 왜냐면 매번 '가장 비용이 적은 노드'를 선택해서 임의의 과정을 반복하기 때문
* 그리디 알고리즘 : 현재 상황에서 가장 좋아보이는 것만 선택하는 알고리즘
과정
1. 출발 노드를 설정
2. 최단 거리 테이블 초기화(무한으로)
3. 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드 선택
4. 해당 노드를 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블 갱신
5. 위 과정에서 3, 4번 반복
- 다익스트라는 각 노드에 대한 현재까지의 최단거리 정보를 항상 1차원 리스트에 저장하며 리스트를 계속 갱신한다는 특징이 있다
- 매번 현재 처리하고 있는 노드를 기준으로 주변 간선을 확인한다. 나중에 현재 처리하고 있는 노드와 인접한 노드로 도달하는 더 짧은 경로를 찾으면 더 짧은 경로가 있다는걸 확인하고 갱신
- 반복할 때마다 특정 노드까지의 최단거리를 확정한다.


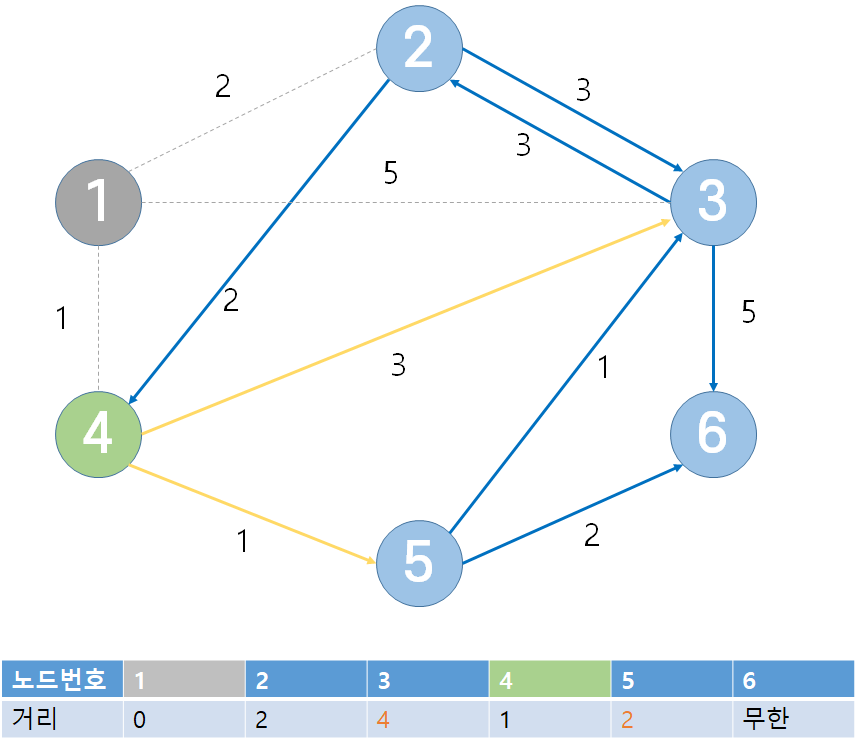



- 한 단계당 하나의 노드에 대한 최단 거리를 확실히 찾는다
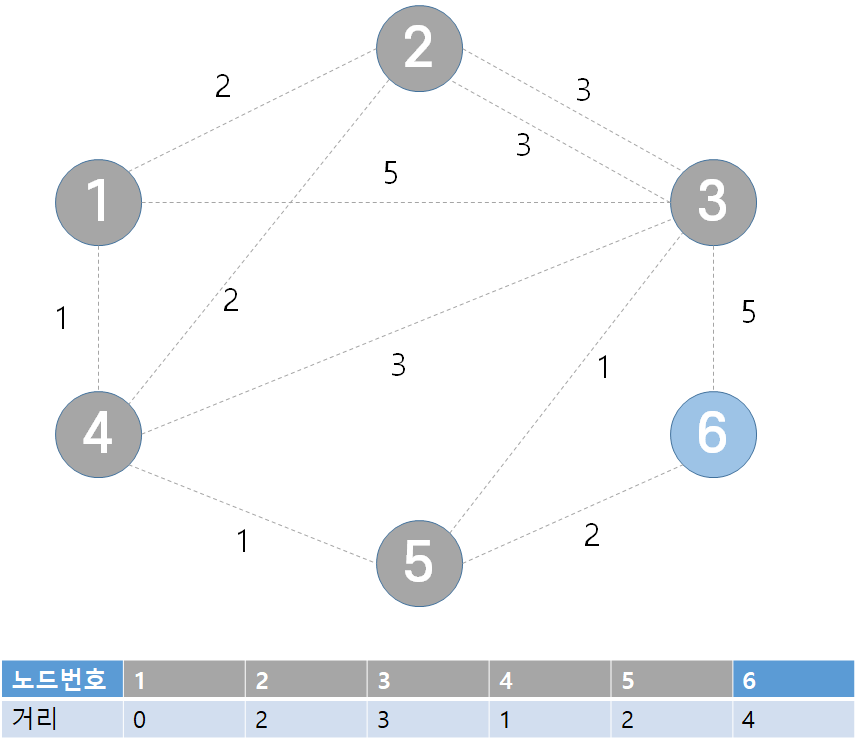
- 사실 마지막 노드에 대해서는 더이상 테이블이 갱신될 수 없기 때문에 다른 노드로 가는 경우 확인할 필요가 없음
- 한번 처리된 노드의 최단 거리는 고정되어 더이상 바뀌지 않고 한 단계당 하나의 노드에 대한 최단 거리 확실히 찾은 것으로 이해하면 된다 !
간단한 다익스트라 코드
- 선형탐색을 이용한 코드
- 시간복잡도 O(V^2)
- 노드 개수 5000개 이하면 위 코드 사용가능, 하지만 10000개가 넘어가면 해결하기 어려움
- 시간복잡도를 줄이려면 우선순위 큐를 사용해야한다
import sys
input = sys.stdin.readline
INF = int(1e9) # 무한을 의미하는 값으로 10억 설정
# 노드의 개수, 간손의 개수 입력받기
n, m = map(int, input().split())
# 시작 노드 번호를 입력받기
start = int(input())
# 각 노드에 연결되어 있는 노드에 대한 정보를 담는 리스트를 만들기
graph = [[] for _ in range(n + 1)]
# 방문한 적이 있는지 체크하는 목적의 리스트
visited = [False] * (n+1)
# 최단 거리 테이블을 모두 무한으로 초기화
distance = [INF] * (n+1)
print(graph, visited, distance)
# 모든 간선 정보 입력받기
for _ in range(m):
a, b, c = map(int, input().split())
# a번 노드에서 b번 노드로 가는 비용이 c라는 의미
graph[a].append((b, c))
print(graph)
# 방문하지 않은 노드 중에서 가장 최단 거리가 짧은 노드의 번호를 반환
def get_smallest_node():
min_value = INF
index = 0 # 가장 최단 거리가 짧은 노드(idx)
for i in range(1, n+1):
# 거리가 min_value보다 작고 방문하지 않았으면
if distance[i] < min_value and not visited[i]:
min_value = distance[i]
index = i
return index
def dijkstra(start):
# 시작 노드에 대해서 초기화
distance[start] = 0
visited[start] = True
for j in graph[start]:
distance[j[0]] = j[1]
# 시작 노드를 제외한 전체 n-1개의 노드에 대해 반복
for i in range(n-1):
# 현재 최단 거리가 가장 짧은 노드를 꺼내서 방문처리
now = get_smallest_node()
visited[now] = True
# 현재 노드와 연결된 다른 노드를 확인
for j in graph[now]:
cost = distance[now] + j[1]
# 현재 노드를 거쳐서 다른 노드로 이동하는 거리가 더 짧은 경우
if cost < distance[j[0]]:
distance[j[0]] = cost
# 다익스트라 알고리즘 수행
dijkstra(start)
# 모든 노드로 가기 위한 최단 거리를 출력
for i in range(1, n+1):
# 도달할 수 없는 경우, 무한이라고 출력
if distance[i] == INF:
print("INFINITY")
# 도달할 수 있는 경우 거리를 출력
else:
print(distance[i])
개선된 다익스트라 알고리즘
우선순위 큐를 이용한 다익스트라 알고리즘
- 최악의 상황에도 시간 복잡도 O(ElogV) 보장
- 힙은 모든 원소를 저장한 뒤에 우선순위에 맞게 빠르게 뽑아낼 수 있어 우선순위 큐를 구현하는데 가장 많이 사용된다
- 우선순위 큐를 이용해 시작 노드로부터 '거리'가 짧은 노드 순서대로 큐에서 나올 수 있도록 다익스트라 알고리즘 작성
우선순위 큐에 대해 알고싶으시면 이 포스팅을 참고해주세요
[이론/자료구조] - 우선순위 큐와 heap - python
우선순위 큐와 heap - python
참고 | 이코테2021 | 우선순위 큐 우선순위 큐 우선순위가 가장 높은 데이터를 가장 먼저 삭제하는 자료구조 우선순위 큐는 데이터를 우선순위에 따라 처리하고 싶을 때 사용 ex) 물건 데이터를 자
ssafy-story.tistory.com
구현 방식
1. 출발 노드를 설정
2. 최단 거리 테이블 초기화(무한으로), 우선순위 큐 초기화
3. 현재 선택된 노드와 연결된 노드들 우선순위 큐에 담기(거리, 노드)
4. 우선순위 큐에 담겨있는 원소 중 하나 꺼내기
5. 해당 노드를 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블 갱신
6. 위 과정에서 3, 4, 5번 반복
- 쉬운 이해를 위해 위에서 봤던 그래프를 다시 참고해보겠습니다

우선순위 큐
| (거리:1, 노드: 4) | (거리:2, 노드: 2) | (거리:5, 노드: 3) |
- 이와 같은 방식으로 진행되며, 순서는 간단한 다익스트라를 구현했을 때와 동일합니다
코드 구현
- 파이썬에서 표준 라이브러리로 heapq를 제공하여 min-heapify를 쉽게 구현할 수 있습니다
- 우선순위 큐에서 나오는 첫번째 원소는 항상 거리가 짧은 원소가 먼저 나옵니다
- 간단한 다익스트라 코드에 있는 get_smallest_node()는 사용하지 않아도 된다. 왜냐면 최단 거리가 가장 짧은 노드를 선택하는 과정을 다익스트라 최단 경로 함수안에서 우선순위 큐를 이용하는 방식으로 대체할 수 있기 때문이다
import sys
import heapq
input = sys.stdin.readline
INF = 987654321
# 노드 개수, 간선 개수 입력받기
n, m = map(int, input().split())
# 시작 노드 번호 입력받기
start = int(input())
# 각 노드에 연결되어 있는 노드에 대한 정보를 담는 리스트 만들기
graph = [[] for i in range(n+1)]
# 최단 거리 테이블을 모두 무한으로 초기화
distance = [INF] * (n+1)
# 모든 간선 정보를 입력받기
for _ in range(m):
a, b, c = map(int, input().split())
# a번 노드에서 b번 노드로 가는 비용이 c라는 의미
graph[a].append((b, c))
print(graph)
def dijkstra(start):
q = []
# 시작 노드로 가기 위한 최단 경로는 0으로 설정하여 큐에 삽입
heapq.heappush(q, (0, start))
distance[start] = 0
while q: # 큐가 비어있지 않다면
# 가장 최단 거리가 짧은 노드에 대한 정보 꺼내기
dist, now = heapq.heappop(q)
# 현재 노드가 이미 처리된 적이 있는 노드라면 무시
if distance[now] < dist:
continue
# 현재 노드와 연결된 다른 인접한 노드들을 확인
for i in graph[now]:
# print(i)
cost = dist + i[1]
# 현재 노드를 거쳐서 다른 노드로 이동하는 거리가 더 짧은 경우
if cost < distance[i[0]]:
distance[i[0]] = cost
heapq.heappush(q, (cost, i[0]))
dijkstra(start)
# 모든 노드로 가기 위한 최단 거리를 출력
for i in range(1, n+1):
# 도달할 수 없는 경우, 무한이라고 출력
if distance[i] == INF:
print("INFINITY")
# 도달할 수 있는 경우 거리 출력
else:
print(distance[i], end=" ")
![[최단경로] 다익스트라 - Python](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbFO7uQ%2Fbtq52UtSsKM%2FOtcIt7wnHwyzaoR3a9KV3K%2Fimg.png)