비트 연산자

JS 문제를 풀다가 '|'를 발견하고 당황했다,, 이 기본적인걸 까먹었다니 ㅜㅜ

블로그에 정리하면서 다시 상기시키려 한다

JS에는 다양한 연산자가 존재한다

1. 할당 2. 비교 3. 산술 4. 비트 5. 논리 6. 문자열 7. 조건(삼항) 8. 쉼표 9. 단항 10. 관계

할당과 비교, 산술은 자주 쓰이는 것이므로 정리하지 않고 넘어가려한다

혹시 알고싶은 분은 여기 들어가보시면 됩니다

비트 연산자는 피연산자를 10진수, 16진수, 8진수처럼 취급하지 않고 32비트의 집합으로 취급한다. 예를 들면 10진수의 9는 2진수의 1001로 나타낼 수 있다. 비트 단위 연산자는 이진법으로 연산을 수행하지만 JS의 표준 숫자값을 반환한다.

라고 MDN에 정리가 되어있다

연산자	사용법	name	설명
논리곱	a & b	AND	두 피연산자의 각 자리 비트의 값이 둘 다 1일 경우 해당하는 자리에 1반환
논리합	a \| b	OR	두 피연산자의 각 자리의 비트값이 둘 다 0일 경우 해당하는 자리에 0 반환 (하나라도 1이면 1반환)
베타적 논리합	a ^ b	XOR	두 피연산자의 각 자리 비트의 값이 같을 경우 해당하는 자리에 0을 반환 (두 피연산자의 각 자리 비트의 값이 다를 경우 해당하는 자리에 1을 반환) 1이 홀수개일때 답이 1
부정(전환)	~a	NOT	피연산자의 각 자리의 비트를 뒤집는다 (1-> 0, 0 -> 1)
왼쪽 시프트	a << b	LEFT SHIFT	오른쪽에서 0들을 이동시키면서 a의 이진수의 각 비트를 b비트 만큼 왼쪽으로 이동시킨 값을 반환
부호전파 오른쪽 시프트	a >> b	RIGHT SHIFT	가장 왼쪽 비트의 복사본을 왼쪽에 밀어 오른쪽으로 이동하고, 맨 오른쪽 비트가 떨어져 나간다 (왼쪽에 1이나 0을 채움)
부호없는 오른쪽 시프트	a >>> b	UNSIGNED RIGHT SHIFT	왼쪽에 0을 밀어넣어 오른쪽으로 이동하고, 맨 오른쪽 비트가 떨어져 나갑니다. (왼쪽에 0을 채움)

비트 논리 연산자

32비트 정수로 변환되고 비트(0, 1)의 연속으로 표현된다. 32비트가 넘는 경우 가장 중요한(왼쪽)비트부터 제거된다.

표현	결과	이진법 설명
15 & 9	9	1111 & 1001 = 1001 (둘다 1일경우 1반환, 아니면 0반환)
15 \| 9	15	1111 \| 1001 = 1111 (둘다 0일경우 0반환, 아니면 1반환)
15 ^ 9	6	1111 ^ 1001 = 0110 (둘다 값이 같은 경우 0반환, 아니면 1반환)
~15	-16	1111 => 00001111, 11110000
~9	-10	~00000000... 0000 1001 = 1111 1111 ... 1111 1001

console.log(15 & 9) // 9
console.log(15|9) // 15 
console.log(15^9) // 6 
console.log(~15) // -16 
console.log(~9) // -10

비트 시프트 연산자

첫번째는 이동될 수치이고, 두번째는 첫번째 피연산자가 이동될 비트 자리수를 명시한다

이동 연산자는 피연산자를 32비트의 정수로 변환하고 왼쪽의 피연산자와 같은 형태를 반환한다

표현	결과	설명
5 << 1	10	0101 << 1 = 1010
9 >> 2 -9 >> 2	2 -3	1001 >> 2 => 0010 0000 0000 0000 0000 0000 0000 0000 1001(9) -> 0000 0000 0000 0000 0000 0000 0000 0010 = 2 (10진수) 1111 1111 1111 1111 1111 1111 1111 0111(-9) -> 1111 1111 1111 1111 1111 1111 1111 1101 = -3 (10진수)
9 >>> 2 -9 >>> 2	2 1073741821	0101 >>> 1 = 0010 0000 0000 0000 0000 0000 0000 0000 1001(9) -> 0000 0000 0000 0000 0000 0000 0000 0010 = 2 (10진수) 1111 1111 1111 1111 1111 1111 1111 0111(-9) -> 0011 1111 1111 1111 1111 1111 1111 1101 = 1073741821 (10진수)

console.log(5 << 1) //10
console.log(9 >> 2) //2
console.log(-9 >> 2) //-3
console.log(9 >>> 2) //2
console.log(-9 >>> 2) //1073741821

의문점 : 비트 부정(전환) 연산자(~)

15는 2진수로 바꾸면 1111(2)이다 이를 비트전환연산 하는 경우 0000(2)가 된다 그럼 답은 0이 되는것아닌가?

-16이 나오는걸 보고 검색을 해봤다

이걸 알면 -9 >> 2가 왜 -3이 나오는지도 저절로 깨달을 수 있다

참고

여기1

여기2

여기3

비트 전환 연산자

비트 전환 연산자는 2진수로 표현했을 때 1은 0으로, 0은 1로 바꾸는 연산자다

그리고 정수형에서만 사용가능한 연산자이다.

이렇게 1에서 0으로 0에서 1로 바꾸는것을 1의 보수라고 한다.

다시말해 비트 전환 연산자는 1의 보수로 바꿔주는 연산자라고 할 수 있다.

정수의 표현 in 컴퓨터

컴퓨터에서 정수를 표현하는 방법은 크게 부호없는 정수와 부호있는 정수로 나누어 생각한다

부호없는 정수를 표현할 때에는 단지 해당 정수 크기의 절대값을 2진수로 표현하면 된다.

하지만 문제는 부호있는 정수에서 음수를 표현하는 방법이다

비트 전환 연산자에서 정수는 부호있는 정수라고 생각한다

기본적으로 우리가 사용하는 10진수를 컴퓨터가 받아들일 수 있는 2진수로 표현할 때 최소단위는 1byte를 기준으로 한다. [1byte(8bit) => 여기서 1bit는 0또는 1]

원래는 js는 32bit 피연산자를 사용해서 32bit를 기준으로 해야하지만, 웬만한 큰 값들은 무시하고 8비트만 사용하려한다.

그럼 아까 15를 2진수를 변경하면 1111(2)라 생각했지만 실은 0000 1111(2)였던 것이다

이를 비트 전환 연산을 하게되면 1111 0000(2)가 된다.

그럼 10진수로 바꾼 값은 240이 되는걸까?

이런 오류를 제대로 알기 위해 1의 보수부터 자세히 알아보겠다

1의 보수 : 1을 0으로, 0을 1로?

비트 전환 연산자, 1의 보수가 등장한 이유는 바로 -(음수)를 컴퓨터에서 표현하기 위해서다!!

컴퓨터는 음수라는 숫자는 존재하지 않는다. 그렇게 우리에게 보여줄뿐,,

그럼 컴퓨터가 음수를 처리할 수 있을까? 바로 1의 보수이다

사실 1의 보수는 단순히 0을 1로, 1을 0으로 바꿔주는 것이 전부가 아니라 10진수의 (양의)정수를 음수로 바꿔주는 역할을 하는 것이다!

[1의 보수법 : 양수의 모든 비트를 반전하여 음수를 표현하는 방법]

그리고 실질적인 데이터 값은 8비트 중에 7비트만 사용한다는 사실! 최상위 비트는 +/-를 결정한다고 한다

최상위 비트는 0이면 양수, 1이면 음수를 뜻한다. 이런 맨 앞의 비트를 부호비트(Most Significant Bit, MSB)로 부호를 결정하는 비트라고 한다

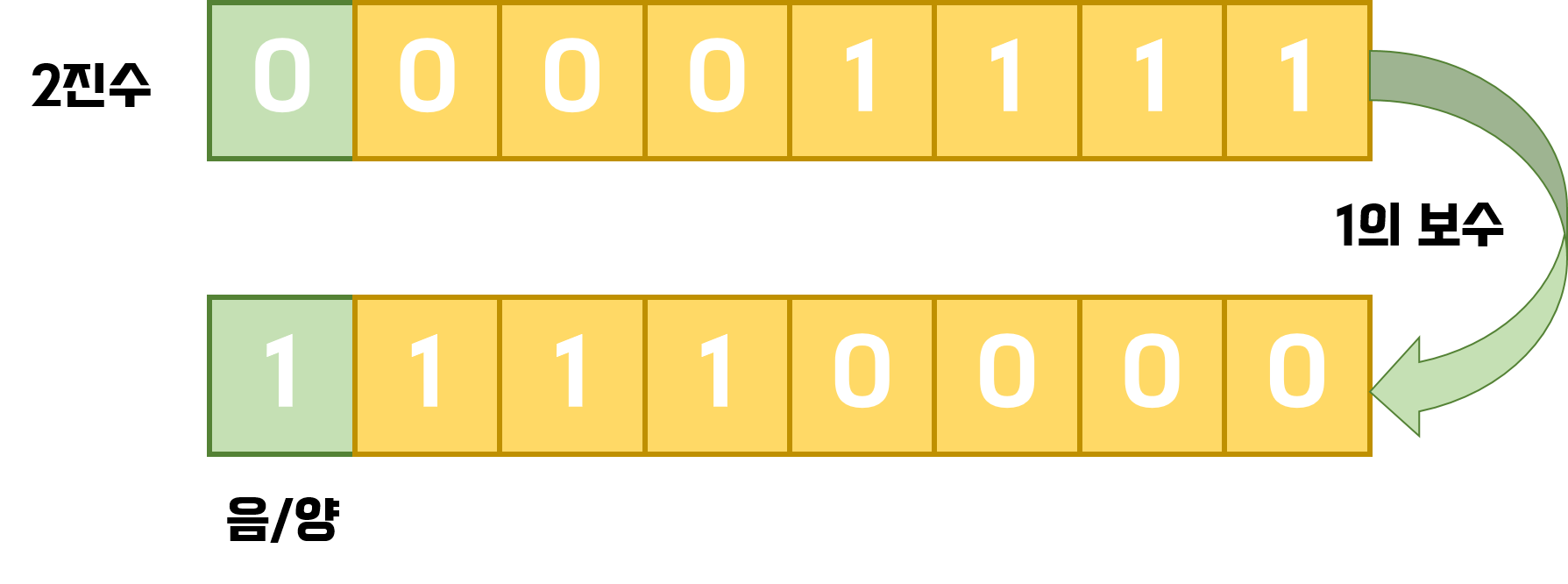
하지만 맨 앞이 부호를 결정하는 비트라고 생각해도 그럼 값을 바꿨을 때 -112가 되는걸까?

이를 더 자세히 알기 위해 2의 보수도 알아보겠다!

2의 보수 : 10진수의 음수형

참고로 2의 보수는 비트 전환 연산의 2진수에 영향을 미치진 않는다 (~15 = 1111 0000(2)이다)

다만 2의 보수는 컴퓨터가 알아보는 10진수의 음수형이라고 설명할 수 있다.

우리가 2진수를 계산하는 방법이랑은 다르다. 컴퓨터만의 계산법이 있음.

컴퓨터는 뺄셈을 못하기 때문에 음수를 표현할 수 없다고 했는데 바로 그 문제를 해결하기 위해 2의 보수를 만들어냈다.

2의 보수를 사용하면 컴퓨터가 바라봤을 때 10진수 15가 -15가 된다는 것이다!

그럼 2의 보수는 어떻게 만드는걸까?

2의 보수는 1의 보수에서 더하기 1을 하면 된다!

11110001이 컴퓨터가 인식하는 -15가 된다는 것이다.

사람은 2의 보수를 봤을 때 알아보기 힘들다. 컴퓨터가 봤을 때 저 1111 0001은 -15가 되는 것이다

그럼 어떻게 -16이 나왔을까?

(2의 보수는 (2^8 - a = 241, a=15)를 2진수로 바꾼 값으로 표현할 수 있다. 값은 똑같이 1111 0001이 나온다)

참고로 우리가 원하는 -16은 2의 보수를 취했을 때, 0001 0000 => 1110 1111 => 1111 0000이 나오게 됨

결론은?

1111 0001는 컴퓨터가 바라봤을 때 -15로 인식한다

하지만 우리는 왜 -16이 나왔는지 알아봐야한다

비트 전환 연산 | 1의 보수을 사용했을 경우

15 = 0000 1111

~15 = 1111 0000 (not 연산으로 0->1, 1->0으로 변환됨) - 1의 보수

2의 보수 사용 | 컴퓨터가 음수로 표현하는 수

16 = 0001 0000

-16 = 1111 0000 (2^8 - 16으로 계산한 결과) - 2의 보수

위의 결과에서 ~15와 컴퓨터의 음수 표현방법인 2의 보수를 사용했을 때 값이 같은걸 볼 수 있다

~15(1111 0000) = -16(1111 0000)이므로

~15 = -16이 되는 것이다

그냥 피연산자 값에 1을 더하고 -부호만 붙여주면 비트 부정 연산의 10진수값이라고 외우면 될 것 같기도,,

이 비트부정연산을 언제 사용하는진 잘 모르겠지만,, 나의 호기심을 해결하기 위해 정리했다

너무 시간을 많이 쏟은 것 같기도 하지만.. 뿌듯

나와 같이 이 문제에 대해 의문을 가지는 사람들에게 도움이 되면 좋겠다